Z085 - Zestaw do doświadczeń z optyki geometrycznej

Zestaw zawiera trzy modele (w postaci bloków akrylowych) soczewek (wypukłej, wklęsłej i płaskowypukłej), pryzmat prostokątny oraz pryzmat trapezowy, płytkę równoległościenną, kuwetę półcylindryczną do pomiaru współczynnika załamania cieczy oraz elastyczne zwierciadło. 

Za pomocą zestawu uczniowie mogą wykonywać doświadczenia indywidualnie lub w grupach, ustawiając modele układów optycznych na blatach stołów lub szkolnych ławek.

Zestaw może być używany również do doświadczeń pokazowych, ponieważ jego elementy są przystosowane do mocowania na szkolnych tablicach magnetycznych.

W skład zestawu wchodzą:

• laser pięciowiązkowy (przełącznikiem można włączyć jedną, trzy lub pięć wiązek);
• blok akrylowy - model soczewki dwuwypukłej;
• blok akrylowy - model soczewki płaskowypukłej;
• blok akrylowy - model soczewki dwuwklęsłej;
• pryzmat prostokątny;
• pryzmat trapezowy;
• płytka równoległościenna;
• elastyczne zwierciadło, które (po odpowiednim ustawieniu) może być zwierciadłem płaskim, wklęsłym lub wypukłym (o regulowanym promieniu krzywizny);
• kuweta półcylindryczna;
• wykonana z folii magnetycznej tarcza Kolbego;
• zasilacz sieciowy.

Wszystkie elementy składowe zestawu są umieszczone w niewielkiej plastikowej walizce.

Zestaw można uzupełnić o zasilacz bateryjny (zestaw nr 115) – również przystosowany do magnetycznego mocowania na tablicy magnetycznej. W zasilaczu można stosować baterie lub akumulatory typu AA. Użycie zasilacza bateryjnego zamiast zasilacza sieciowego znacznie ułatwia wykonanie doświadczeń w sytuacji, gdy w pobliżu tablicy nie ma gniazdka instalacji elektrycznej. Dodatkowo zwiększa bezpieczeństwo uczniów samodzielnie wykonujących doświadczenia.

Tarcza Kolbego, model soczewki dwuwypukłej oraz laser pięciowiązkowy wraz z zasilaczem bateryjnym umieszczone na szkolnej tablicy magnetycznej.

Przykładowe doświadczenia:

Obserwacja odbicia światła od zwierciadła płaskiego

Promienie światła padające na powierzchnię zwierciadła płaskiego pod różnymi kątami. Kąt odbicia jest równy kątowi padania.

Wiązka promieni równoległych padających na powierzchnię zwierciadła płaskiego. Wiązka, po odbiciu od powierzchni zwierciadła, pozostaje wiązką promieni równoległych.

Obserwacja odbicia światła od zwierciadła wklęsłego; pomiar ogniskowej zwierciadła

Wiązka promieni równoległych padająca na powierzchnię cylindrycznego zwierciadła wklęsłego (przekrój zwierciadła kulistego). Promienie, po odbiciu od powierzchni zwierciadła, tworzą wiązkę promieni zbieżnych, przecinających się w ognisku zwierciadła. Za pomocą skali tarczy Kolbego można zmierzyć ogniskową zwierciadła (w podanym przykładzie 34±1 mm).

Obserwacja odbicia światła od zwierciadła wypukłego

Na zwierciadło wklęsłe pada wiązka promieni równoległych. Promienie, po odbiciu od powierzchni zwierciadła, tworzą wiązkę promieni rozbieżnych.

Obserwacja przejścia wiązki światła przez płytkę płaskorównoległą

Na płytkę pada wiązka promieni równoległych. Po przejściu przez płytkę wiązka pozostaje wiązką promieni równoległych. Gdy promienie nie padają na powierzchnię płytki prostopadle, ulegają przesunięciu bez zmiany kierunku.

Obserwacja przejścia promieni światła przez cienką soczewkę dwuwypukłą, pomiar ogniskowej, zjawisko abberacji sferycznej

Promień światła biegnący wzdłuż osi optycznej soczewki

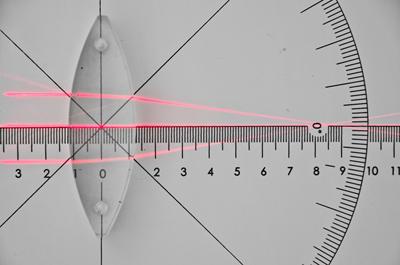
Wiązka promieni równoległych (przyosiowych – biegnących w niewielkiej, w porównaniu z promieniem krzywizny powierzchni soczewki, odległości od osi soczewki) przechodząca przez soczewkę. Promienie przecinają się w jednym punkcie – ognisku soczewki. Ogniskowa w podanym przykładzie wynosi 84±1 mm.

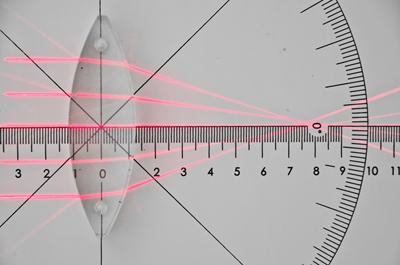
Wiązka promieni równoległych przechodząca przez soczewkę. Promienie przyosiowe przecinają się, po przejściu przez soczewkę, w innym punkcie niż promienie biegnące w większej odległości od osi optycznej – zjawisko abberacji sferycznej.

Obserwacja przejścia promieni światła przez soczewkę płaskowypukłą (grubą)

Promienie światła przechodzące przez soczewkę płaskowypukłą. Wyraźnie widoczne zjawisko abberacji sferycznej. Widać także promienie odbite od powierzchni soczewek (światło padające na granicę ośrodków częściowo odbija się, a częściowo przechodzi – z tym zjawiskiem „walczą” konstruktorzy obiektywów fotograficznych; światło odbite od powierzchni soczewek w obiektywie tworzy na zdjęciu barwne plamy, gdy w polu widzenia obiektywu znajduje się silne źródło światła).

Obserwacja przejścia promieni światła przez soczewkę dwuwklęsłą

Wiązka promieni równoległych po przejściu przez soczewkę dwuwklęsłą staje się wiązką promieni rozbieżnych. Na zdjęciu widoczne są również promienie odbite od powierzchni soczewki.

Obserwacja przejścia promieni światła przez układ soczewek cienkich

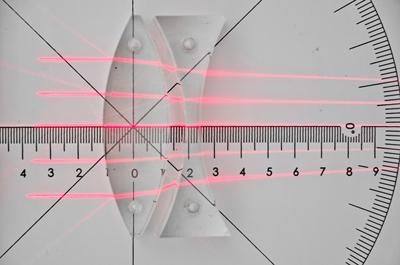
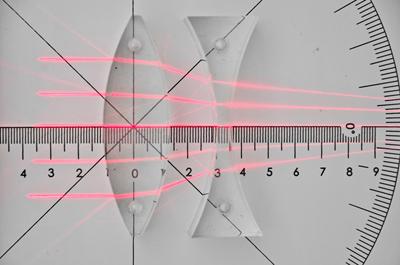
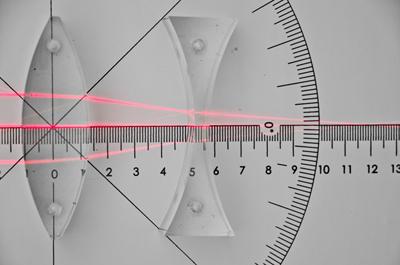
Wiązka promieni równoległych przechodząca przez układ soczewek. Ogniskowa układu zależy nie tylko od ogniskowych soczewek, ale również od odległości między soczewkami.

Obserwacja przejścia wiązki światła przez pryzmat

Obserwacja całkowitego wewnętrznego odbicia w pryzmacie prostokątnym

Obserwacja całkowitego wewnętrznego odbicia w pryzmacie prostokątnym – model szkła odblaskowego

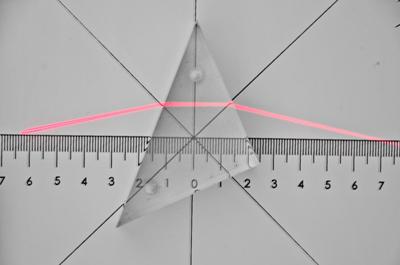
Promień światła pada na pryzmat, dwukrotnie ulega w pryzmacie całkowitemu wewnętrznemu odbiciu i powraca w kierunku źródła światła.

Pomiar wartości współczynnika załamania dla materiału, z którego jest wykonany półkolisty blok akrylowy – model płaskowypukłej soczewki grubej

Promień światła pada na powierzchnię „walcową” modelu soczewki wzdłuż jej osi optycznej.

Promień światła pada na powierzchnię „walcową” modelu soczewki pod kątem ostrym do jej osi optycznej.

Zwiększamy kąt pomiędzy padającym promieniem światła a osią optyczną. Widoczne są wychodzący promień załamany oraz promień odbity od powierzchni płaskiej bloku akrylowego.

Jeszcze bardziej zwiększamy kąt pomiędzy padającym promieniem światła a osią optyczną. Widoczny jest tylko promień odbity od powierzchni płaskiej bloku akrylowego. Kąt padania jest większy od kąta granicznego. Zachodzi zjawisko całkowitego wewnętrznego odbicia.

Zmieniając kąt pomiędzy promieniem padającym a osią optyczną modelu soczewki, poszukujemy kąta granicznego, dla którego promień odbity i załamany pokrywają się (promień wychodzący z bloku akrylowego biegnie wzdłuż jego płaskiej krawędzi).

Obliczamy wartość współczynnika załamania.
Uwaga: w omawianym doświadczeniu promień pada na blok akrylowy prostopadle do jego walcowej powierzchni.

Obserwacja przejścia wiązki światła przez pryzmat trapezowy

Wygląd produktu na zdjęciu może odbiegać od wyglądu produktu w rzeczywistości.